RC Hochpass Rechner
Berechnung von Frequenzgang, Dämpfung und Phasenverschiebung eines RC-Hochpasses
RC-Hochpass Filter verstehen
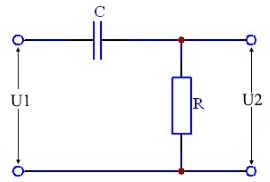
Ein RC-Hochpass ist ein Filter, der hohe Frequenzen durchlässt und niedrige Frequenzen dämpft. Er besteht aus einem Kondensator C in Serie mit dem Eingang und einem Widerstand R parallel zum Ausgang. Die Grenzfrequenz bestimmt, ab welcher Frequenz das Signal weniger als -3dB gedämpft wird.
🎯 Grenzfrequenz fg
Kritische Frequenz bei -3dB Dämpfung:
fg = 1/(2πRC)
🔊 Dämpfung in dB
Logarithmisches Amplitudenverhältnis:
AdB = 20 × log(U2/U1)
📐 Phasenverschiebung
Winkel zwischen Ein- und Ausgang:
φ = arctan(1/(ωRC))
📈 Frequenzverhalten
- • f << fg: Starke Dämpfung (~-20dB/Dekade)
- • f = fg: -3dB Dämpfung
- • f >> fg: Keine Dämpfung (0dB)
Grundformeln des RC-Hochpasses
📊 Übertragungsfunktion
Die Ausgangsspannung in Abhängigkeit der Frequenz:
\[ U_2 = U_1 \cdot \frac{2\pi f R C}{\sqrt{1 + (2\pi f R C)^2}} \]
Oder vereinfacht mit bekanntem XC:
\[ U_2 = U_1 \cdot \frac{R}{\sqrt{R^2 + X_C^2}} \]
🔧 Dämpfung und Phasengang
Dämpfung in Dezibel und Phasenverschiebung:
\[ A_{dB} = 20 \cdot \log_{10}\left(\frac{\omega R C}{\sqrt{1 + (\omega R C)^2}}\right) \] \[ \phi = \arctan\left(\frac{1}{\omega R C}\right) \]
Wobei: ω = 2πf (Kreisfrequenz)
Praktische Beispiele
📝 Beispiel 1: Audio-Hochpass
Aufgabe: Bass-Filter für Lautsprecher, fg = 80 Hz
Gegeben: R = 100 Ω, gesucht: C = ?
Berechnung:
\[ C = \frac{1}{2\pi f_g R} = \frac{1}{2\pi \cdot 80 \cdot 100} = 19,9 \, \mu F \]
Ergebnis: 20 μF Kondensator filtert Frequenzen unter 80 Hz heraus.
📝 Beispiel 2: HF-Kopplung
Aufgabe: AC-Kopplung für 1 kHz Signal
Gegeben: R = 1 kΩ, C = 160 nF, f = 1 kHz
Berechnung:
\[ f_g = \frac{1}{2\pi \cdot 1000 \cdot 160 \times 10^{-9}} = 995 \, Hz \]
Bei 1 kHz: Dämpfung ≈ -3dB, Phasenverschiebung ≈ 45°
Ergebnis: Signal wird minimal gedämpft, DC wird blockiert.
Schaltbild und Frequenzgang
📈 Frequenzgang-Eigenschaften
- • f = 0.1×fg: -20dB Dämpfung
- • f = fg: -3dB Dämpfung
- • f = 10×fg: -0.1dB Dämpfung
- • Flanke: +20dB/Dekade
📐 Phasengang-Eigenschaften
- • f → 0: φ → +90°
- • f = fg: φ = +45°
- • f → ∞: φ → 0°
- • Ausgang eilt vor
Praktische Anwendungen
🎵 Audio-Technik
- • Bass-Absenkung in Lautsprechern
- • Subsonic-Filter
- • Mikrofonverstärker
- • Equalizer-Schaltungen
📡 Elektronik
- • AC-Kopplung zwischen Stufen
- • DC-Blocker
- • Differenzierer-Schaltungen
- • EMV-Filter
💡 Praktische Tipps:
- Dimensionierung: fg etwa 10x niedriger als niedrigste Nutzfrequenz wählen
- Phasenverschiebung: Bei Audio-Anwendungen beachten (Laufzeitunterschiede)
- Kondensator-Typ: Für Audio Folien- oder Elektrolytkondensatoren verwenden
- Lastimpedanz: Nachfolgende Schaltung sollte R >> RLast erfüllen
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode