LR-Hochpass Rechner

Berechnung von LR-Hochpassfiltern: Ausgangsspannung, Dämpfung, Phasenverschiebung und Grenzfrequenz


📈 LR-Hochpass

Induktiver Hochpassfilter - lässt hohe Frequenzen durch

ℹ️
Hinweis: Der LR-Hochpass lässt hohe Frequenzen durch und dämpft niedrige Frequenzen. Bei der Grenzfrequenz beträgt die Dämpfung -3dB und die Phasenverschiebung +45°.
⚠️ Fehler:

Geben Sie die Werte für Widerstand R, Induktivität L, Frequenz f und Eingangsspannung U ein und klicken Sie auf Berechnen um die Hochpass-Eigenschaften zu ermitteln.


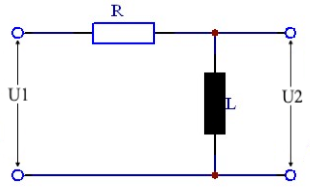
LR-Hochpass Schaltbild

LR-Hochpass verstehen

Ein LR-Hochpass ist ein induktiver Filter, der hohe Frequenzen durchlässt und niedrige Frequenzen dämpft. Er besteht aus einer Induktivität L in Serie und einem Widerstand R parallel zum Ausgang. Die Grenzfrequenz fg = R/(2πL) bestimmt das Filterverhalten.

📈 Hochpass-Verhalten

Übertragungsverhalten:

\(H(jω) = \frac{jωL}{R + jωL}\)
Hohe Frequenzen werden durchgelassen
📉 Ausgangsspannung

Spannungsteiler-Prinzip:

\(U_2 = U_1 \cdot \frac{X_L}{\sqrt{R^2 + X_L^2}}\)
XL = 2πfL (Blindwiderstand)
🔄 Phasenverhalten

Phasenverschiebung:

\(φ = \arctan\left(\frac{R}{X_L}\right)\)
Bei fg: φ = 45°, bei f >> fg: φ → 0°
📊 Grenzfrequenz

-3dB-Punkt:

\(f_g = \frac{R}{2πL}\)
Bei fg: R = XL, Dämpfung = -3dB

Grundformeln des LR-Hochpasses

📊 Übertragungsverhalten

Die fundamentalen Formeln für LR-Hochpassfilter:

\[U_2 = U_1 \cdot \frac{2πfL}{\sqrt{R^2 + (2πfL)^2}}\] \[V_u = 20 \cdot \log_{10}\left(\frac{U_2}{U_1}\right) \text{ [dB]}\] \[φ = \arctan\left(\frac{R}{ωL}\right) \text{ [°]}\]

Dabei ist: ω = 2πf, XL = ωL

🔧 Grenzfrequenz und Dimensionierung

Auslegung von LR-Hochpassfiltern:

\[f_g = \frac{R}{2πL}\] \[R = 2πf_g L\] \[L = \frac{R}{2πf_g}\]

Bei fg: |H| = 1/√2 ≈ 0,707 (-3dB), φ = 45°

Praktische Beispiele

📝 Beispiel 1: Audio-Hochpass für Mitteltöner

Aufgabe: Hochpass für Mitteltöner-Lautsprecher bei 800 Hz
Gegeben: fg = 800 Hz, Lautsprecherimpedanz R = 8 Ω
Berechnung:

\[L = \frac{R}{2πf_g} = \frac{8}{2π \cdot 800} = 1,59 \text{ mH}\] \[\text{Bei 1,6 kHz: } X_L = 2π \cdot 1600 \cdot 1,59 \times 10^{-3} = 16 \text{ Ω}\]

Ergebnis: L = 1,59 mH (1,5 mH E12) für Mitteltöner-Weiche.

📝 Beispiel 2: HF-Entkopplung in Verstärkern

Aufgabe: Hochpass für Operationsverstärker-Eingang bei 100 Hz
Gegeben: fg = 100 Hz, Eingangswiderstand R = 10 kΩ
Berechnung:

\[L = \frac{10000}{2π \cdot 100} = 15,9 \text{ H}\] \[\text{Praktisch: Spule zu groß, RC-Hochpass verwenden!}\]

Ergebnis: LR-Hochpass bei niedrigen Frequenzen unpraktisch - RC-Lösung bevorzugen.

Frequenzgang und Phasenverhalten

Hochpass Phasengang
📈 Amplitudengang
  • • f ≪ fg: Starke Dämpfung (-20dB/Dekade)
  • • f = fg: -3dB Dämpfung
  • • f ≫ fg: Keine Dämpfung (0dB)
  • • Rolloff: +20dB/Dekade unter fg
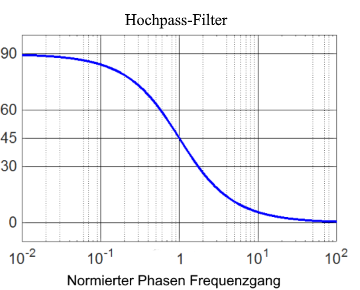
🔄 Phasengang
  • • f ≪ fg: φ ≈ +90° (induktiv)
  • • f = fg: φ = +45°
  • • f ≫ fg: φ ≈ 0° (resistiv)
  • • Übergang: Kontinuierlich von +90° zu 0°

Praktische Anwendungen

🎵 Audio-Technik
  • • Lautsprecher-Frequenzweichen
  • • Mitteltöner- und Hochtöner-Filter
  • • Subwoofer-Schutz vor hohen Frequenzen
  • • Professionelle PA-Systeme
⚡ Leistungselektronik
  • • Motordrosseln und Netzfilter
  • • Stromsensor-Entkopplung
  • • EMV-Filter für Schaltnetzteile
  • • Differentialmode-Filterung
💡 Praktische Tipps:
  • Induktivität-Wahl: Ferritkerne für Audio, Luftspulen für HF
  • Güte-Faktor: Q = ωL/R bestimmt die Flankensteilheit
  • Sättigung: Kernmaterial darf bei Maximalstrom nicht sättigen
  • Niederfrequenz: LR-Hochpass bei fg < 1 kHz meist unpraktisch

Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand

Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)

Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz

Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator

Kondensatoren und Spulen

Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung

Gleichrichter- und Dioden

Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode