Ampermeter Parallelwiderstand Rechner
Rechner und Formeln zur Berechnung des Parallelwiderstands beim Ampermeter
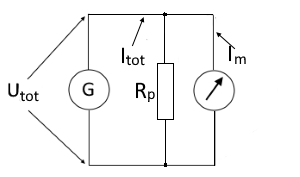
Schaltbild eines Ampermeters mit Parallelwiderstand (Shunt) zur Messbereichserweiterung
Hinweis zur Bedienung: Geben Sie den gewünschten Gesamtstrom und den Vollausschlagstrom des Messwerks ein. Wählen Sie dann entweder den Messwerkwiderstand oder die Gesamtspannung. Der Rechner berechnet den erforderlichen Parallelwiderstand (Shunt) und dessen Verlustleistung.
Wichtige Eigenschaften des Parallelwiderstands:
- Messbereichserweiterung: Ermöglicht Messung höherer Ströme
- Stromteiler: Rp und Rm bilden einen Stromteiler
- Shunt-Funktion: Hauptstrom fließt durch den niederohmigen Shunt
- Schutzfunktion: Verhindert Überlastung des empfindlichen Messwerks
Grundbegriffe einfach erklärt
Ampermeter-Parallelwiderstand (Shunt): "Bypass für Hauptstrom"
Ein Parallelwiderstand (Shunt) wird parallel zu einem Ampermeter geschaltet, um dessen Messbereich zu erweitern.
Der größte Teil des Stroms fließt durch den niederohmigen Shunt, nur ein kleiner Anteil durch das Messwerk.
Messbereichserweiterung: "Höhere Ströme mit demselben Messwerk messen"
Durch den Parallelwiderstand kann ein 100mA-Messwerk beispielsweise 10A oder 100A messen.
Das Stromteilerverhältnis bestimmt den Erweiterungsfaktor.
Stromteilerprinzip: "Kontrollierte Stromaufteilung"
Parallelwiderstand und Messwerk bilden einen Stromteiler. Der niederohmige Shunt
übernimmt den Hauptstrom, das Messwerk nur seinen Nennanteil.
Praktische Anwendungsbeispiele
Beispiel 1 - Labor-Amperemeter-Erweiterung:
"100mA Messwerk auf 10A erweitern, Rm = 50Ω:"
Erweiterungsfaktor: n = 10A/0.1A = 100
Rp = Rm/(n-1) = 50Ω/99 = 0.505Ω
Shunt-Strom: 10A - 0.1A = 9.9A → Leistung: 49.5W
Beispiel 2 - Automotive-Batteriemonitor:
"50A Batterieladestrom mit 75mV/50mA Messwerk messen:"
Rm = 75mV/50mA = 1.5Ω
n = 50A/0.05A = 1000
Rp = 1.5Ω/999 = 1.5mΩ → sehr niederohmiger Shunt erforderlich
Beispiel 3 - Industrielle Strommessung:
"500A Maschinenstrom mit 5A-Messwerk messen:"
Erweiterungsfaktor: n = 500A/5A = 100
Bei Rm = 0.1Ω: Rp = 0.1Ω/99 = 1.01mΩ
Shunt-Leistung: (495A)² × 0.00101Ω = 247W → Kühlung erforderlich!
Shunt-Typen und Anwendungen
| Shunt-Typ | Strombereich | Spannungsabfall | Anwendung |
|---|---|---|---|
| Manganin-Shunt | 1A - 1000A | 50mV - 150mV | Präzisionsmessungen |
| Kupfer-Shunt | 10A - 10kA | 50mV - 100mV | Industrieanwendungen |
| Dickfilm-Shunt | 100mA - 10A | 50mV - 200mV | SMD-Anwendungen |
| Stromwandler | 5A - 5kA | 5A Sekundär | Hochstrom-AC-Messung |
| Hall-Sensor | 1A - 1kA | Isoliert | Galvanisch getrennte Messung |
Anwendungsgebiete von Ampermeter-Parallelwiderständen
Messtechnik und Laborgeräte:
- Multimeter: Messbereichsumschaltung in analogen Geräten
- Oszilloskope: Stromsonden mit verschiedenen Bereichen
- Panel-Meter: Anpassung an verschiedene Strombereiche
- Datenlogger: Eingangsbeschaltung für Stromsensoren
Industrielle Anwendungen:
- Motorüberwachung: Strommessung in Antrieben
- Schweißgeräte: Schweißstrom-Überwachung
- Batteriesysteme: Lade-/Entladestrom-Messung
- Photovoltaik: DC-String-Strom-Überwachung
Formeln zum Ampermeter-Parallelwiderstand
Grundformeln
Parallelwiderstand über Erweiterungsfaktor: \[\displaystyle R_p = \frac{R_m}{n-1} \quad \text{mit} \quad n = \frac{I_{tot}}{I_m}\]
Parallelwiderstand direkt: \[\displaystyle R_p = \frac{R_m \times I_m}{I_{tot} - I_m}\]
Parallelwiderstand über Gesamtspannung: \[\displaystyle R_p = \frac{U_{tot}}{I_{tot} - I_m}\]
Stromteiler-Formeln
Gesamtwiderstand der Parallelschaltung: \[\displaystyle R_{ges} = \frac{R_m \times R_p}{R_m + R_p}\]
Stromaufteilung: \[\displaystyle I_m = I_{tot} \times \frac{R_p}{R_m + R_p}\] \[\displaystyle I_p = I_{tot} \times \frac{R_m}{R_m + R_p}\]
Leistungsberechnungen
Verlustleistung im Shunt: \[\displaystyle P_p = I_p^2 \times R_p = (I_{tot} - I_m)^2 \times R_p\]
Verlustleistung im Messwerk: \[\displaystyle P_m = I_m^2 \times R_m = U_{tot} \times I_m\]
Legende:
- \(I_{tot}\) - Gesamtstrom, zu messender Maximalstrom (A)
- \(I_m\) - Messwerkstrom, Vollausschlagstrom (A)
- \(I_p\) - Strom durch Parallelwiderstand (A)
- \(R_p\) - Parallelwiderstand, Shunt-Widerstand (Ω)
- \(R_m\) - Messwerkwiderstand, Innenwiderstand (Ω)
- \(U_{tot}\) - Spannung über der Parallelschaltung (V)
- \(P_p\) - Verlustleistung im Shunt (W)
- \(n\) - Erweiterungsfaktor (dimensionslos)
Rechenbeispiel 1: Standard-Multimeter
Messwerk: 1mA/100Ω, erweitern auf 10A: Erweiterungsfaktor: \[n = \frac{10A}{1mA} = 10000\] Parallelwiderstand: \[R_p = \frac{100Ω}{10000-1} = \frac{100Ω}{9999} = 10.001mΩ\] Shunt-Strom bei Vollausschlag: \[I_p = 10A - 1mA = 9.999A\] Verlustleistung im Shunt: \[P_p = (9.999A)^2 \times 10.001mΩ = 1W\]
Rechenbeispiel 2: Hochstrom-Messsung
Aufgabe: 500A messen mit 75mV/50mA Standard-Shunt: Messwerkwiderstand: \[R_m = \frac{75mV}{50mA} = 1.5Ω\] Für 500A Messbereich: \[R_p = \frac{1.5Ω \times 0.05A}{500A - 0.05A} = \frac{0.075}{499.95} = 0.15mΩ\] Shunt-Leistung: \[P_p = (499.95A)^2 \times 0.15mΩ = 37.5kW\] (!) → In der Praxis: 75mV-Shunt direkt verwenden!
Praktische Designregeln
Shunt-Dimensionierung:
- Materialwahl: Manganin für Präzision, Kupfer für hohe Ströme
- Spannungsabfall: Standard 50mV, 75mV oder 150mV
- Kühlung: Ausreichende Wärmeableitung bei hohen Leistungen
- Vier-Leiter-Technik: Separate Strom- und Spannungsanschlüsse
Sicherheitsaspekte:
- Kurzschlussfestigkeit: Shunt muss Fehlerstrom verkraften
- Thermische Überlastung: Temperaturüberwachung bei hohen Strömen
- Isolation: Berührungsschutz bei gefährlichen Spannungen
- Alterung: Langzeitstabilität des Shunt-Materials
Hochstrom-Messtechnik
Herausforderungen bei hohen Strömen:
Bei Strömen über 100A entstehen besondere Anforderungen:
Wärmeableitung:
Die Verlustleistung im Shunt steigt quadratisch mit dem Strom:
\[P = I^2 \times R\]
Massive Kühlkörper oder Wasserkühlung werden erforderlich.
Vier-Leiter-Messung:
Bei niederohmigen Shunts sind Leitungswiderstände relevant:
- Stromzuführung mit dicken Leitern
- Spannungsmessung mit separaten, dünnen Leitern
AC vs. DC Strommessung
DC-Strommessung:
- Einfache Ohm'sche Shunts ausreichend
- Konstanter Widerstand über weiten Temperaturbereich
- Lineare Kennlinie über gesamten Messbereich
AC-Strommessung:
- Frequenzverhalten des Shunts beachten
- Skin-Effekt bei hohen Frequenzen
- Stromwandler oft besser geeignet
Moderne Alternativen zu Shunts
Hall-Effekt-Sensoren:
- Galvanische Trennung: Kein direkter Stromkreis
- AC/DC-fähig: Misst beide Stromarten
- Kein Spannungsabfall: Verlustfrei
- Nachteile: Temperaturdrift, Offset
Rogowski-Spulen:
- Berührungslos: Umschlingen des Leiters
- Keine Sättigung: Sehr hohe Ströme messbar
- AC-Messung: Nur für Wechselströme
- Integration erforderlich: di/dt-Signal
Kalibrierung und Abgleich
Shunt-Kalibrierung:
Präzisions-Shunts werden bei definierter Temperatur kalibriert:
Referenzstrom-Verfahren:
- Bekannten Referenzstrom durch Shunt leiten
- Spannungsabfall mit Präzisions-Voltmeter messen
- Shunt-Widerstand berechnen: R = U/I
- Bei verschiedenen Stromwerten wiederholen (Linearität)
Temperaturkoeffizient:
Manganin: ≈ ±15ppm/°C
Kupfer: ≈ +3900ppm/°C
→ Temperaturkompensation bei Präzisionsmessungen erforderlich
Fehlerquellen und Troubleshooting
Häufige Probleme:
- Falsche Skalierung: Shunt-Widerstand nicht korrekt berechnet
- Überhitzung: Zu kleine Leistungsreserve
- Kontaktprobleme: Hochohmige Verbindungen bei Spannungsmessung
- Alterung: Widerstandswert ändert sich über Zeit
Fehlerbehebung:
- Widerstandsmessung: Shunt ohne Strom prüfen
- Referenzmessung: Mit kalibriertem Referenz-Amperemeter vergleichen
- Thermische Prüfung: Temperaturverhalten kontrollieren
- Kontaktprüfung: Übergangswiderstand der Anschlüsse messen
Der Ampermeter-Parallelwiderstand (Shunt) ist ein fundamentales Element in der elektrischen Strommessung. Er ermöglicht die sichere und präzise Messung von Strömen, die weit über dem natürlichen Messbereich empfindlicher Messwerke liegen. Die korrekte Berechnung und Dimensionierung unter Berücksichtigung von Leistungsverlusten, Kühlung und Materialauswahl ist essentiell für zuverlässige Strommessungen in Labor, Industrie und Leistungselektronik.
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode