Voltmeter Vorwiderstand Rechner
Rechner und Formeln zur Berechnung des Vorwiderstands für Messbereichserweiterung
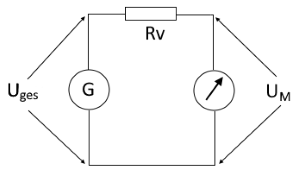
Schaltbild eines Voltmeters mit Vorwiderstand zur Messbereichserweiterung
Hinweis zur Bedienung: Geben Sie die gewünschte Gesamtspannung und die Nennspannung des Messwerks ein. Wählen Sie dann entweder den Messwerkwiderstand oder den Messwerkstrom. Der Rechner berechnet den erforderlichen Vorwiderstand und dessen Verlustleistung.
Wichtige Eigenschaften des Vorwiderstands:
- Messbereichserweiterung: Ermöglicht Messung höherer Spannungen
- Spannungsteiler: Rv und Rm bilden einen Spannungsteiler
- Schutzfunktion: Verhindert Überlastung des empfindlichen Messwerks
- Linearitätserhaltung: Proportionale Skalierung des Messbereichs
Grundbegriffe einfach erklärt
Voltmeter-Vorwiderstand: "Schutzwiderstand für empfindliche Messwerke"
Ein Vorwiderstand wird in Reihe zu einem Voltmeter geschaltet, um dessen Messbereich zu erweitern.
Er begrenzt den Strom durch das empfindliche Messwerk auf einen sicheren Wert.
Messbereichserweiterung: "Höhere Spannungen mit demselben Messwerk messen"
Durch den Vorwiderstand kann ein 10V-Messwerk beispielsweise 100V oder 1000V messen.
Das Teilerverhältnis bestimmt den Erweiterungsfaktor.
Spannungsteilerprinzip: "Kontrollierte Spannungsaufteilung"
Vorwiderstand und Messwerk bilden einen Spannungsteiler. Der größere Vorwiderstand
übernimmt den Hauptteil der Spannung, das Messwerk nur seinen Nennanteil.
Praktische Anwendungsbeispiele
Beispiel 1 - Labor-Multimeter-Erweiterung:
"10V Messwerk auf 1000V erweitern, Rm = 10kΩ:"
Erweiterungsfaktor: n = 1000V/10V = 100
Rv = (n-1) × Rm = 99 × 10kΩ = 990kΩ
Gesamtwiderstand: 1MΩ → sehr hochohmig, minimale Rückwirkung
Beispiel 2 - Automotive-Anwendung:
"12V-Bordnetz überwachen mit 50mV/1mA Messwerk:"
Für 15V Maximalspannung: Rm = 50mV/1mA = 50Ω
Rv = (15V/0.05V - 1) × 50Ω = 299 × 50Ω = 14.95kΩ
Praktischer Wert: 15kΩ (E12-Reihe)
Beispiel 3 - Hochspannungs-Messtechnik:
"Netzspannung 230V mit 5V-Panel-Meter messen:"
Sicherheitsfaktor 1.5: Umax = 230V × 1.5 = 345V
Bei Rm = 10kΩ: Rv = (345V/5V - 1) × 10kΩ = 680kΩ
Leistung: Pv = (345V-5V)²/690kΩ = 167mW
Messwerk-Typen und -Parameter
| Messwerk-Typ | Typische Spannung | Typischer Strom | Anwendung |
|---|---|---|---|
| Drehspul-Instrument | 50mV - 1V | 50µA - 1mA | Präzisionsmessungen DC |
| Digital-Panel-Meter | 200mV - 20V | 1µA - 20mA | Moderne Anzeigen |
| Drehspul-Mikro | 10mV - 100mV | 10µA - 100µA | Hochempfindliche Messungen |
| LED-Bargraph | 2V - 5V | 2mA - 20mA | Pegelanzeigen |
| Analog-IC-Meter | 1V - 10V | 1mA - 10mA | IC-basierte Systeme |
Anwendungsgebiete von Voltmeter-Vorwiderständen
Messtechnik und Laborgeräte:
- Multimeter: Messbereichsumschaltung in analogen Geräten
- Oszilloskope: Eingangsteiler für verschiedene V/div-Einstellungen
- Panel-Meter: Anpassung an verschiedene Messbereiche
- Datenlogger: Eingangsbeschaltung für verschiedene Sensoren
Industrielle Anwendungen:
- Prozessüberwachung: Anzeige von Betriebsspannungen
- Schaltanlagen: Spannungsanzeige in Verteilern
- USV-Systeme: Batteriespannungsüberwachung
- Photovoltaik: String-Spannungsüberwachung
Formeln zum Voltmeter-Vorwiderstand
Grundformeln
Vorwiderstand über Messwerkwiderstand: \[\displaystyle R_v = \left(\frac{U_{ges}}{U_m} - 1\right) \times R_m\]
Vorwiderstand über Messwerkstrom: \[\displaystyle R_v = \frac{U_{ges} - U_m}{I_m}\]
Erweiterungsfaktor: \[\displaystyle n = \frac{U_{ges}}{U_m} = \frac{R_v + R_m}{R_m}\]
Leistungsberechnungen
Verlustleistung im Vorwiderstand: \[\displaystyle P_v = I_m^2 \times R_v = \frac{(U_{ges} - U_m)^2}{R_v}\]
Gesamtleistung der Schaltung: \[\displaystyle P_{ges} = U_{ges} \times I_m = I_m^2 \times (R_v + R_m)\]
Umkehrformeln
Messwerkwiderstand bei gegebenem Vorwiderstand: \[\displaystyle R_m = \frac{R_v \times U_m}{U_{ges} - U_m}\]
Maximalspannung bei gegebenem Vorwiderstand: \[\displaystyle U_{ges} = U_m \times \left(1 + \frac{R_v}{R_m}\right)\]
Legende:
- \(U_{ges}\) - Gesamtspannung, zu messende Maximalspannung (V)
- \(U_m\) - Messwerkspannung, Nennspannung des Messwerks (V)
- \(R_v\) - Vorwiderstand (Ω)
- \(R_m\) - Messwerkwiderstand, Innenwiderstand (Ω)
- \(I_m\) - Messwerkstrom, Vollausschlagstrom (A)
- \(P_v\) - Verlustleistung im Vorwiderstand (W)
- \(n\) - Erweiterungsfaktor (dimensionslos)
Rechenbeispiel 1: Standard-Multimeter
Messwerk: 1V/50µA, erweitern auf 1000V: Messwerkwiderstand: \[R_m = \frac{U_m}{I_m} = \frac{1V}{50µA} = 20kΩ\] Erweiterungsfaktor: \[n = \frac{1000V}{1V} = 1000\] Vorwiderstand: \[R_v = (n-1) \times R_m = 999 \times 20kΩ = 19.98MΩ\] Verlustleistung bei Vollausschlag: \[P_v = I_m^2 \times R_v = (50µA)^2 \times 19.98MΩ = 50mW\]
Rechenbeispiel 2: Panel-Meter für Netzteil
Aufgabe: 5V Panel-Meter für 0-30V Netzteil, Rm = 10kΩ: Vorwiderstand: \[R_v = \left(\frac{30V}{5V} - 1\right) \times 10kΩ = 5 \times 10kΩ = 50kΩ\] Messstrom: \[I_m = \frac{U_m}{R_m} = \frac{5V}{10kΩ} = 0.5mA\] Leistung bei 30V: \[P_v = \frac{(30V-5V)^2}{50kΩ} = \frac{625V^2}{50kΩ} = 12.5mW\] Praktische Wahl: 51kΩ (E12), 0.25W Widerstand
Praktische Designregeln
Widerstandsauswahl:
- Toleranz: 1% für Messanwendungen, 5% für Anzeigen
- Leistung: Mindestens 2× berechnete Verlustleistung
- Spannungsfestigkeit: Widerstand muss Gesamtspannung vertragen
- Temperaturkoeffizient: Niedrig für stabile Messungen
Sicherheitsaspekte:
- Überspannungsschutz: 20-50% Sicherheitsfaktor einplanen
- Isolation: Ausreichende Kriech- und Luftstrecken
- Gehäuse: Berührungsschutz bei Hochspannung
- Sicherung: Zusätzlicher Schutz vor Überstrom
Hochspannungs-Vorwiderstände
Besondere Anforderungen:
Bei hohen Spannungen (>1kV) sind spezielle Maßnahmen erforderlich:
Widerstandsketten:
Aufteilung auf mehrere Widerstände zur Spannungsverteilung:
\[R_{v,gesamt} = \sum_{i=1}^n R_{v,i}\]
Jeder Teilwiderstand: Rv,i ≤ Umax,Widerstand/Im
Kompensationskondensatoren:
Parallel zu jedem Widerstand zur Frequenzkompensation bei AC-Messungen.
Frequenzverhalten und AC-Messungen
AC-Spannungsmessung:
Bei Wechselspannungen müssen zusätzliche Faktoren berücksichtigt werden:
Effektivwert-Messung: \[U_{eff} = \frac{U_{Scheitel}}{\sqrt{2}}\] Der Vorwiderstand muss für den Scheitelwert dimensioniert werden!
Frequenzgang:
Parasitäre Kapazitäten können bei hohen Frequenzen das Teilerverhältnis beeinflussen.
Digitale vs. analoge Messwerke
Analoge Messwerke:
- Konstanter Eingangswiderstand: Unabhängig vom Messbereich
- Lineare Skalierung: Einfache Umrechnung
- Rückwirkungsarm: Bei richtig dimensioniertem Vorwiderstand
Digitale Panel-Meter:
- Hoher Eingangswiderstand: Meist >1MΩ
- Integrierte Teiler: Oft programmierbare Bereiche
- Überlastschutz: Meist integriert
Kalibrierung und Abgleich
Präzisions-Einstellung:
Für genaue Messungen ist oft ein Abgleich erforderlich:
Trimm-Potentiometer: \[R_{v,total} = R_{v,fest} + R_{trimm}\] Typisch: 95% Festwiderstand + 5% Trimmer
Kalibrierung:
- Referenzspannung anlegen (z.B. 90% der Maximalspannung)
- Anzeige mit Referenzmessgerät vergleichen
- Trimmer justieren bis zur exakten Anzeige
- Bei mehreren Messpunkten prüfen (Linearität)
Fehlerquellen und Troubleshooting
Häufige Probleme:
- Falsche Skalierung: Vorwiderstand nicht korrekt berechnet
- Temperaturgang: Verschiedene TK von Rv und Rm
- Alterung: Widerstandswerte ändern sich über Zeit
- Überlastung: Zu kleine Leistungsreserve
Fehlerbehebung:
- Widerstandsmessung: Rv und Rm einzeln prüfen
- Referenzmessung: Mit kalibriertem Gerät vergleichen
- Isolationsprüfung: Kriechströme ausschließen
- Thermische Prüfung: Verhalten bei Temperaturänderung
Der Voltmeter-Vorwiderstand ist ein fundamentales Element in der elektrischen Messtechnik. Er ermöglicht die sichere und präzise Messung von Spannungen, die weit über dem natürlichen Messbereich empfindlicher Messwerke liegen. Die korrekte Berechnung und Dimensionierung unter Berücksichtigung von Sicherheitsfaktoren, Toleranzen und Umgebungsbedingungen ist essentiell für zuverlässige Messungen in Labor, Industrie und Entwicklung.
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode