T-Dämpfungsglied Rechner
Rechner und Formeln zur Berechnung der Widerstände eines T-Dämpfungsglied
Hinweis zur Bedienung: Wählen Sie die Berechnungsmethode (dB-Dämpfung oder Spannungsverhältnis), geben Sie die Systemimpedanz und die entsprechenden Werte ein. Der Rechner berechnet die beiden Widerstandswerte R₁ (Serie) und R₂ (Parallel) für das T-Dämpfungsglied.
Standard-Impedanzen:
- 50Ω: Standard in der Hochfrequenztechnik (Funk, Mobilfunk)
- 75Ω: Standard in der Videotechnik (Antenne, Kabel-TV)
- 600Ω: Standard in der professionellen Audiotechnik
- 100Ω: Differenzielle Signale (Ethernet, USB)
Grundbegriffe einfach erklärt
T-Dämpfungsglied: "Effiziente Signaldämpfung mit minimaler Leistungsverschwendung"
Das T-Dämpfungsglied bietet im Vergleich zum π-Glied geringere Verlustleistung, da der
Querwiderstand höhere Werte hat und weniger Strom führt.
Serienwiderstände R₁: "Direkter Signalweg mit kontrollierter Dämpfung"
Diese beiden identischen Widerstände liegen im Signalweg und bestimmen zusammen mit R₂ die Gesamtdämpfung.
Parallelwiderstand R₂: "Querableitung zur Impedanzanpassung"
Dieser Widerstand zur Masse sorgt für die korrekte Impedanz und vervollständigt das Dämpfungsnetzwerk.
Praktische Anwendungsbeispiele
Beispiel 1 - HF-Verstärker-Entkopplung:
"50Ω-System, 10dB Dämpfung zwischen Verstärkerstufen:"
a = 10^(10/20) = 3.16
R₁ = 50Ω × (3.16 - 1) ÷ (3.16 + 1) = 26.0Ω
R₂ = 50Ω × (2 × 3.16) ÷ (3.16² - 1) = 39.8Ω
Beispiel 2 - Audio-Line-Dämpfung:
"600Ω-Audio-System, 12dB Dämpfung (Faktor 4):"
R₁ = 600Ω × (4 - 1) ÷ (4 + 1) = 360Ω
R₂ = 600Ω × (2 × 4) ÷ (4² - 1) = 320Ω
Beispiel 3 - Video-Signal-Dämpfung:
"75Ω-Video-System, 6dB Dämpfung (Faktor 2):"
R₁ = 75Ω × (2 - 1) ÷ (2 + 1) = 25Ω
R₂ = 75Ω × (2 × 2) ÷ (2² - 1) = 100Ω
T-Glied vs. π-Glied Vergleich
| Eigenschaft | T-Dämpfungsglied | π-Dämpfungsglied |
|---|---|---|
| Aufbau | 2 Serien-, 1 Parallelwiderstand | 2 Parallel-, 1 Serienwiderstand |
| Verlustleistung | Geringer (höhere R₂-Werte) | Höher (niedrige R₂-Werte) |
| Impedanzanpassung | Gut bei niedrigen Dämpfungen | Besser bei hohen Dämpfungen |
| Widerstandswerte | R₁ < Z, R₂ > Z | R₁ > Z, R₂ ≈ Z |
| Typische Anwendung | Verstärker-Entkopplung | Messgeräte-Eingänge |
Anwendungsgebiete des T-Glieds
Bevorzugte Einsatzgebiete:
- Verstärker-Zwischenstufen: Minimale Verlustleistung wichtig
- Signalgeneratoren: Ausgangsleistung optimieren
- Audio-Equipment: Geringere Wärmeentwicklung
- Batteriegeräte: Energieeffizienz maximieren
Typische Dämpfungswerte:
- 3dB (Faktor 1.41): Standard-Halbierung
- 6dB (Faktor 2): Häufige Pegelanpassung
- 10dB (Faktor 3.16): Verstärker-Entkopplung
- 20dB (Faktor 10): Starke Dämpfung
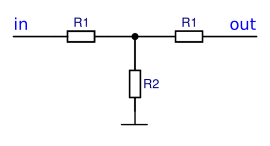
Schaltbild eines T-Dämpfungsglieds
Formeln zum T-Dämpfungsglied
Grundformeln
Dämpfungsfaktor aus dB-Wert: \[\displaystyle a = \frac{U_1}{U_2} = 10^{\frac{\Delta L_{dB}}{20}}\]
Dämpfungsfaktor aus Spannungsverhältnis: \[\displaystyle a = \frac{U_{ein}}{U_{aus}}\]
Widerstandsberechnung
Serienwiderstände R₁: \[\displaystyle R_1 = Z \times \frac{a - 1}{a + 1}\]
Parallelwiderstand R₂: \[\displaystyle R_2 = Z \times \frac{2a}{a^2 - 1}\]
Legende:
- \(a\) - Dämpfungsfaktor (linear)
- \(\Delta L_{dB}\) - Dämpfung in Dezibel
- \(Z\) - Systemimpedanz (Ω)
- \(R_1\) - Serienwiderstände (Ω)
- \(R_2\) - Parallelwiderstand (Ω)
- \(U_1, U_{ein}\) - Eingangsspannung
- \(U_2, U_{aus}\) - Ausgangsspannung
Rechenbeispiel 1: Standard HF-T-Glied
50Ω-System, 6dB Dämpfung: \[a = 10^{6/20} = 1.995 \approx 2\] \[R_1 = 50\Omega \times \frac{2 - 1}{2 + 1} = 50\Omega \times \frac{1}{3} = 16.67\Omega\] \[R_2 = 50\Omega \times \frac{2 \times 2}{2^2 - 1} = 50\Omega \times \frac{4}{3} = 66.67\Omega\]
Rechenbeispiel 2: Audio-T-Glied
600Ω-Audio-System, 20dB Dämpfung: \[a = 10^{20/20} = 10\] \[R_1 = 600\Omega \times \frac{10 - 1}{10 + 1} = 600\Omega \times \frac{9}{11} = 490.9\Omega\] \[R_2 = 600\Omega \times \frac{2 \times 10}{10^2 - 1} = 600\Omega \times \frac{20}{99} = 121.2\Omega\]
Erweiterte Berechnungen
Verlustleistung im T-Glied:
Die Verlustleistung ist geringer als beim π-Glied, da R₂ größere Werte hat:
\[\displaystyle P_{R2} = \frac{U_{R2}^2}{R_2}\]
Bei höheren R₂-Werten ist diese Verlustleistung deutlich reduziert.
Impedanztransformation:
Das T-Glied kann auch zur Impedanztransformation verwendet werden:
\[\displaystyle Z_{ein} = Z_{aus} = Z \text{ (bei symmetrischer Auslegung)}\]
Praktische Dimensionierung
Widerstandsauswahl:
- R₁-Werte: Meist kleiner als die Systemimpedanz
- R₂-Werte: Meist größer als die Systemimpedanz
- Leistungsverteilung: R₁ führt mehr Strom als R₂
Leistungsberechnung:
Die Serienwiderstände R₁ müssen die höchste Leistung verkraften:
\[\displaystyle P_{R1} = I^2 \times R_1\]
\[\displaystyle P_{R2} = \frac{U_{parallel}^2}{R_2}\]
Frequenzverhalten
Breitbandiges Verhalten:
T-Dämpfungsglieder zeigen ähnlich gutes Frequenzverhalten wie π-Glieder:
- DC bis MHz: Konstante Dämpfung
- Parasitäre Effekte: Erst bei sehr hohen Frequenzen
- Layout-Einfluss: Geringer bei kompaktem Aufbau
Dimensionierungsrichtlinien
T-Glied wählen wenn:
- Geringe Verlustleistung erforderlich
- Dämpfung bis etwa 20dB
- Kostengünstige Lösung gesucht
- Kompakter Aufbau möglich
π-Glied bevorzugen wenn:
- Sehr hohe Dämpfungen (>20dB)
- Beste Impedanzanpassung erforderlich
- Maximale Isolation gewünscht
- Messgeräteeingänge
Toleranz-Einfluss
Auswirkung von Widerstandstoleranzen:
- Dämpfungsabweichung: ±5% Widerstand → ±0.5dB Dämpfung
- Impedanzfehlanpassung: Verschlechterte Rückflussdämpfung
- Präzisionsanwendungen: 1% oder 0.1% Widerstände erforderlich
Aufbau-Optimierung
Layout-Considerations:
- Kurze Verbindungen: Minimale parasitäre Induktivitäten
- Symmetrischer Aufbau: Gleiche Leitungslängen
- Abschirmung: Bei kritischen Anwendungen
- Wärmeableitung: Für Hochleistungsanwendungen
Anpassungsnetzwerke
Asymmetrische T-Glieder:
Für Impedanztransformation zwischen verschiedenen Systemimpedanzen:
\[\displaystyle R_1 = \sqrt{Z_1 \times Z_2} \times \frac{\sqrt{a} - 1}{\sqrt{a} + 1}\]
\[\displaystyle R_2 = \frac{2\sqrt{Z_1 \times Z_2 \times a}}{a - 1}\]
Qualitätskontrolle
Messparameter:
- Dämpfung: S₂₁-Parameter mit Netzwerkanalysator
- Rückflussdämpfung: S₁₁ und S₂₂-Parameter
- Frequenzgang: Konstanz über den Nutzbereich
- Phasenverhalten: Lineare Phase bei Breitbandanwendungen
Das T-Dämpfungsglied ist besonders vorteilhaft, wenn geringe Verlustleistung und Energieeffizienz im Vordergrund stehen. Seine einfache Struktur mit nur drei Widerständen macht es zur kostengünstigen Alternative zum π-Glied, besonders bei niedrigen bis mittleren Dämpfungswerten.
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode