Widerstand Parallelschaltung Rechner
Rechner und Formeln zur Berechnung parallelgeschalteter Widerstände
Hinweis zur Bedienung: Geben Sie alle Widerstandswerte mit Semikolon getrennt in das Eingabefeld ein. Alle Werte müssen in der gleichen Maßeinheit (Ω, kΩ, MΩ) angegeben werden. Der Gesamtwiderstand wird in derselben Einheit ausgegeben.
Wichtige Eigenschaften bei N Parallelwiderständen:
- Gesamtwiderstand: Immer kleiner als der kleinste Einzelwiderstand
- Stromaufteilung: Umgekehrt proportional zu den Widerstandswerten
- Spannung: An allen Widerständen identisch
- Redundanz: Ausfall eines Widerstands beeinträchtigt andere nicht
Grundbegriffe einfach erklärt
N-Parallelschaltung: "Viele parallele Wege für den Strom"
Bei N parallelen Widerständen hat der Strom N verschiedene Wege. Je mehr parallele Wege,
desto kleiner wird der Gesamtwiderstand - wie bei mehreren parallel verlaufenden Rohren.
Leitwert-Addition: "Die Summe der Leitfähigkeiten"
Statt Widerstände zu addieren, werden bei Parallelschaltung die Leitwerte (1/R) addiert.
Mehr parallele Widerstände = höhere Gesamtleitfähigkeit = niedrigerer Gesamtwiderstand.
Dominanz kleiner Widerstände: "Der kleinste bestimmt das Ergebnis"
Der Gesamtwiderstand wird stark vom kleinsten Einzelwiderstand beeinflusst.
Ein sehr kleiner parallel geschalteter Widerstand kann das Gesamtergebnis dominieren.
Praktische Anwendungsbeispiele
Beispiel 1 - LED-Array mit Vorwiderständen:
"4 LEDs mit Vorwiderständen 330Ω, 470Ω, 680Ω, 1kΩ parallel:"
1/Rges = 1/330 + 1/470 + 1/680 + 1/1000 = 0.00303 + 0.00213 + 0.00147 + 0.001 = 0.00763
Rges = 1/0.00763 = 131Ω → Deutlich niedriger als jeder Einzelwiderstand
Beispiel 2 - Heizwiderstände parallel:
"3 Heizwiderstände 100Ω, 150Ω, 200Ω bei 230V parallel:"
Rges = 1/(1/100 + 1/150 + 1/200) = 1/(0.01 + 0.0067 + 0.005) = 46.15Ω
Gesamtleistung: P = U²/R = 230²/46.15 = 1146W (höher als jeder Einzelwiderstand)
Beispiel 3 - Gleichwerte parallel für niedrigeren Widerstand:
"4 × 100Ω parallel für 25Ω Gesamtwiderstand:"
Rges = 100Ω/4 = 25Ω → Einfache Regel bei gleichen Widerständen
Spezialfälle und Optimierungen
| Anzahl gleicher Widerstände | Formel | Beispiel (100Ω) | Gesamtwiderstand |
|---|---|---|---|
| 2 parallel | Rges = R/2 | 2 × 100Ω | 50Ω |
| 3 parallel | Rges = R/3 | 3 × 100Ω | 33.33Ω |
| 4 parallel | Rges = R/4 | 4 × 100Ω | 25Ω |
| n parallel | Rges = R/n | n × 100Ω | 100Ω/n |
Anwendungsgebiete von N-Parallelwiderständen
Elektronik und Schaltungsdesign:
- Widerstandswerte erzeugen: Kombination vorhandener Werte für spezielle Werte
- Stromaufteilung: Definierte Stromverteilung auf mehrere Zweige
- Leistungsverteilung: Aufteilung hoher Leistungen auf mehrere Widerstände
- Redundanz: Ausfallsicherheit durch mehrere parallele Pfade
Praktische Installationen:
- Beleuchtungssysteme: Mehrere Lampen parallel an einer Spannung
- Heizsysteme: Mehrere Heizelemente für höhere Gesamtleistung
- Mess- und Prüftechnik: Präzise Widerstandswerte durch Kombination
- Batteriesysteme: Parallelschaltung von Innenwiderständen
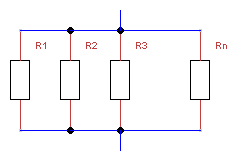
Schaltbild einer Parallelschaltung mehrerer Widerstände
Formeln zur N-Parallelschaltung
Grundformeln
Allgemeine Leitwert-Addition: \[\displaystyle \frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ... + \frac{1}{R_n}\]
Summenformel mit Summenzeichen: \[\displaystyle \frac{1}{R_{ges}} = \sum_{i=1}^n \frac{1}{R_i}\]
Gesamtwiderstand: \[\displaystyle R_{ges} = \frac{1}{\sum_{i=1}^n \frac{1}{R_i}}\]
Spezialfälle
N gleiche Widerstände parallel: \[\displaystyle R_{ges} = \frac{R}{n}\] wobei R der Wert jedes einzelnen Widerstands und n die Anzahl ist.
Zwei Widerstände (Produktformel): \[\displaystyle R_{ges} = \frac{R_1 \times R_2}{R_1 + R_2}\]
Drei Widerstände (erweiterte Produktformel): \[\displaystyle R_{ges} = \frac{R_1 \times R_2 \times R_3}{R_1 R_2 + R_1 R_3 + R_2 R_3}\]
Legende:
- \(R_{ges}\) - Gesamtwiderstand der Parallelschaltung (Ω)
- \(R_1, R_2, ..., R_n\) - Einzelwiderstände (Ω)
- \(n\) - Anzahl der parallelen Widerstände
- \(G_i = 1/R_i\) - Leitwert des i-ten Widerstands (S)
Rechenbeispiel 1: Vier verschiedene Widerstände
Widerstände: 30Ω, 60Ω, 20Ω, 120Ω parallel: \[\frac{1}{R_{ges}} = \frac{1}{30} + \frac{1}{60} + \frac{1}{20} + \frac{1}{120}\] \[\frac{1}{R_{ges}} = 0.0333 + 0.0167 + 0.05 + 0.0083 = 0.1083\] \[R_{ges} = \frac{1}{0.1083} = 9.23\Omega\] Verifikation: Kleinster Widerstand ist 20Ω → Rges < 20Ω ✓
Rechenbeispiel 2: Fünf gleiche Widerstände
5 × 100Ω parallel: \[R_{ges} = \frac{100\Omega}{5} = 20\Omega\] Alternative Berechnung: \[\frac{1}{R_{ges}} = 5 \times \frac{1}{100\Omega} = \frac{5}{100} = 0.05\] \[R_{ges} = \frac{1}{0.05} = 20\Omega\] ✓
Erweiterte Berechnungen
Stromaufteilung bei N Widerständen:
Der Strom durch den i-ten Widerstand:
\[\displaystyle I_i = I_{ges} \times \frac{R_{ges}}{R_i}\]
Leistungsverteilung:
Leistung im i-ten Widerstand:
\[\displaystyle P_i = \frac{U^2}{R_i}\]
Gesamtleistung:
\[\displaystyle P_{ges} = \sum_{i=1}^n P_i = U^2 \times \sum_{i=1}^n \frac{1}{R_i}\]
Praktische Dimensionierungsregeln
Zielwiderstand durch Parallelschaltung erreichen:
- Methode 1: Verwende zwei große Widerstände für kleinen Zielwert
- Methode 2: Verwende viele gleiche Widerstände (Rziel = Reinzel/n)
- Methode 3: Kombiniere vorhandene E-Reihen-Werte optimal
Leistungsaufteilung optimieren:
Für gleichmäßige Leistungsverteilung sollten alle Widerstände gleich groß sein.
Bei unterschiedlichen Werten tragen kleinere Widerstände überproportional zur Gesamtleistung bei.
Approximationen und Näherungen
Dominanz-Regel:
Wenn ein Widerstand viel kleiner ist als alle anderen (Rmin << Randere), dann:
\[R_{ges} \approx R_{min}\]
Schnelle Schätzung:
Rges liegt immer zwischen 0 und dem kleinsten Einzelwiderstand.
Bei gleichen Widerständen: Rges = Reinzel/n
Anwendung in E-Reihen
Standard-Widerstandswerte kombinieren:
- E12-Reihe: 1.0, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, 8.2
- Beispiel: 15Ω gewünscht → 22Ω || 47Ω = 15.7Ω (Abweichung: 4.7%)
- Präzision: Drei Widerstände für höhere Genauigkeit
Toleranz- und Fehlerbetrachtungen
Toleranz-Fortpflanzung:
Bei N Widerständen mit ±5% Toleranz kann der Gesamtwiderstand um ±2% bis ±8% schwanken,
abhängig von der Anzahl und den Werten der Widerstände.
Worst-Case-Analyse:
Für kritische Anwendungen sollten alle Toleranzen in dieselbe Richtung betrachtet werden
(alle minimal oder alle maximal) um die Grenzen zu bestimmen.
Messverfahren und Verifikation
Praktische Messung:
- Einzelmessung: Jeden Widerstand vor dem Einbau messen
- Gesamtmessung: Parallelschaltung messen und mit Berechnung vergleichen
- Fehlersuche: Große Abweichungen deuten auf defekte Widerstände hin
Die Parallelschaltung mehrerer Widerstände ist ein mächtiges Werkzeug zur Erzeugung spezifischer Widerstandswerte, zur Stromaufteilung und zur Leistungsverteilung. Das Verständnis der Leitwert-Addition und der Dominanz kleiner Widerstände ist essentiell für effektives Schaltungsdesign und Problemlösung in der Elektrotechnik.
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode