Spannungsteiler Rechner
Rechner und Formel zur Berechnung eines unbelasteten Spannungsteilers
Hinweis zur Bedienung: Geben Sie genau 3 beliebige Werte ein, um die Berechnung durchzuführen. Mögliche Kombinationen: 2 Spannungen + 1 Widerstand oder 1 Spannung + 2 Widerstände. Die fehlenden Werte werden automatisch berechnet.
Wichtige Eigenschaften des Spannungsteilers:
- Spannungsaufteilung: Proportional zu den Widerstandswerten
- Konstanter Strom: Durch beide Widerstände identisch
- Unbelastet: Keine Last am Ausgang angeschlossen
- Anwendung: Referenzspannungen, Signalpegel, Sensorauswertung
Grundbegriffe einfach erklärt
Spannungsteiler: "Kontrollierte Spannungsreduzierung"
Ein Spannungsteiler besteht aus zwei in Reihe geschalteten Widerständen. Die Eingangsspannung
wird proportional zu den Widerstandswerten aufgeteilt - größerer Widerstand bekommt mehr Spannung.
Teilerverhältnis: "Das Verhältnis bestimmt die Ausgangsspannung"
Das Verhältnis der Widerstände R₁:R₂ bestimmt direkt das Spannungsverhältnis.
Bei gleichen Widerständen wird die Spannung halbiert.
Unbelastet vs. belastet: "Last verändert das Teilerverhältnis"
Ein unbelasteter Spannungsteiler hat keine Last am Ausgang. Bei Belastung wird das
Teilerverhältnis verändert und die Ausgangsspannung sinkt.
Praktische Anwendungsbeispiele
Beispiel 1 - Referenzspannung für ADC:
"5V auf 2.5V halbieren für Mikrocontroller-ADC:"
R₁ = R₂ = 10kΩ → Uout = 5V × (10kΩ/(10kΩ+10kΩ)) = 2.5V
Querstrom: I = 5V/20kΩ = 250µA (niedrig → energiesparend)
Beispiel 2 - Signalpegel-Anpassung:
"10V Signal auf 3.3V reduzieren:"
Gewünschtes Verhältnis: 3.3V/10V = 0.33
R₂/(R₁+R₂) = 0.33 → bei R₂=10kΩ ist R₁=20.3kΩ (E-Wert: 20kΩ)
Beispiel 3 - Batteriespannungs-Überwachung:
"12V Batterie überwachen mit 3.3V ADC:"
Maximale ADC-Spannung: 3.0V bei 14V Batterie (Überladung)
Verhältnis: 3.0V/14V = 0.214 → R₁=39kΩ, R₂=10kΩ
Spannungsteiler-Designregeln
| Anwendung | Querstrom | Widerstandsbereich | Besonderheiten |
|---|---|---|---|
| Referenzspannung | 10-100µA | 10kΩ - 1MΩ | Niedrige Drift, Präzisionswiderstände |
| ADC-Eingänge | 1-10µA | 100kΩ - 10MΩ | Hoher Eingangswiderstand des ADC |
| Signalkonditionierung | 100µA - 1mA | 1kΩ - 100kΩ | Niedrige Ausgangsimpedanz |
| Bias-Spannungen | 10-100µA | 10kΩ - 1MΩ | Temperaturstabilität wichtig |
Anwendungsgebiete des Spannungsteilers
Signalverarbeitung:
- ADC-Eingänge: Signalpegel an ADC-Bereich anpassen
- Referenzspannungen: Stabile Vergleichsspannungen erzeugen
- Offset-Einstellung: DC-Pegel von Signalen verschieben
- Dämpfung: Signale kontrolliert abschwächen
Sensorik und Messtechnik:
- Potentiometer: Variable Spannungsteiler für Einstellungen
- Widerstandssensoren: Temperatur, Druck, Licht
- Batterie-Überwachung: Spannungsmessung mit ADC
- Brückenschaltungen: Präzisionsmessungen
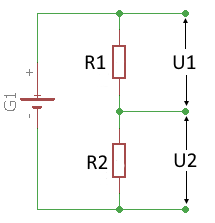
Schaltbild eines unbelasteten Spannungsteilers
Formeln zum Spannungsteiler
Grundformeln
Ausgangsspannung (Hauptformel): \[\displaystyle U_2 = U_{ein} \times \frac{R_2}{R_1 + R_2}\]
Allgemeine Spannungsaufteilung: \[\displaystyle U_i = U_{ges} \times \frac{R_i}{R_{ges}}\]
Teilerverhältnis: \[\displaystyle k = \frac{U_{aus}}{U_{ein}} = \frac{R_2}{R_1 + R_2}\]
Dimensionierungsformeln
R₂ bei gegebenem R₁ und Teilerverhältnis k: \[\displaystyle R_2 = R_1 \times \frac{k}{1-k}\]
R₁ bei gegebenem R₂ und Teilerverhältnis k: \[\displaystyle R_1 = R_2 \times \frac{1-k}{k}\]
Gesamtwiderstand bei gewünschtem Querstrom: \[\displaystyle R_{ges} = \frac{U_{ein}}{I_{quer}}\]
Legende:
- \(U_{ein}, U_{ges}\) - Eingangsspannung (V)
- \(U_{aus}, U_2\) - Ausgangsspannung (V)
- \(U_1\) - Spannung an R₁ (V)
- \(R_1\) - Oberer Widerstand (Ω)
- \(R_2\) - Unterer Widerstand, Ausgangswiderstand (Ω)
- \(R_{ges}\) - Gesamtwiderstand R₁ + R₂ (Ω)
- \(k\) - Teilerverhältnis (dimensionslos)
- \(I_{quer}\) - Querstrom durch den Spannungsteiler (A)
Rechenbeispiel 1: Standard-Spannungsteiler
12V auf 5V reduzieren mit R₁ = 3kΩ: \[k = \frac{5V}{12V} = 0.417\] \[R_2 = 3k\Omega \times \frac{0.417}{1-0.417} = 3k\Omega \times 0.715 = 2.14k\Omega\] Nächster E12-Wert: 2.2kΩ \[U_{aus} = 12V \times \frac{2.2k\Omega}{3k\Omega + 2.2k\Omega} = 5.08V\] (Abweichung: 1.6%) Querstrom: \[I = \frac{12V}{5.2k\Omega} = 2.31mA\]
Rechenbeispiel 2: ADC-Eingangsbeschaltung
15V Batteriespannung für 3.3V ADC mit 10% Reserve: \[U_{ADC,max} = 3.0V \text{ bei } U_{Batt,max} = 16.5V\] \[k = \frac{3.0V}{16.5V} = 0.182\] Mit R₂ = 10kΩ: \[R_1 = 10k\Omega \times \frac{1-0.182}{0.182} = 45k\Omega\] E12-Werte: R₁ = 47kΩ, R₂ = 10kΩ \[U_{ADC} = U_{Batt} \times \frac{10k\Omega}{57k\Omega} = U_{Batt} \times 0.175\] Bei 12V Batterie: UADC = 2.11V ✓
Erweiterte Betrachtungen
Lasteffekt:
Bei Belastung mit RLast parallel zu R₂:
\[\displaystyle R_{2,eff} = \frac{R_2 \times R_{Last}}{R_2 + R_{Last}}\]
Die Ausgangsspannung sinkt entsprechend.
Ausgangsimpedanz:
Die Ausgangsimpedanz des Spannungsteilers:
\[\displaystyle R_{aus} = \frac{R_1 \times R_2}{R_1 + R_2}\]
Sie sollte viel kleiner als die Lastimpedanz sein.
Praktische Designregeln
Querstrom-Dimensionierung:
- Regel: Querstrom 10-100× größer als Laststrom
- Batteriebetrieb: Querstrom < 10µA für lange Laufzeit
- Präzisionsanwendungen: Querstrom > 100µA für Stabilität
Widerstandsauswahl:
- Toleranz: 1% für Präzision, 5% für Standard-Anwendungen
- Temperaturkoeffizient: Gleicher TK für beide Widerstände
- Rauschen: Niederohmige Widerstände für rauscharme Anwendungen
Fehlerquellen und Optimierung
Häufige Probleme:
- Lasteffekt: Ausgangsimpedanz zu hoch für die Last
- Temperaturdrift: Unterschiedliche Temperaturkoeffizienten
- Rauschen: Zu hochohmige Widerstände
- Leistung: Überlastung bei niederohmigen Teilern
Optimierungsansätze:
- Pufferung: Op-Amp als Spannungsfolger nach dem Teiler
- Matched Pairs: Widerstandsnetzwerke mit gleichem TK
- Abschirmung: Bei hochohmigen Teilern gegen Störeinkopplung
Temperatur- und Alterungseffekte
Temperaturverhalten:
Relative Änderung des Teilerverhältnisses:
\[\displaystyle \frac{\Delta k}{k} = \frac{(TK_1 - TK_2) \times \Delta T \times R_1}{R_1 + R_2}\]
wobei TK₁, TK₂ die Temperaturkoeffizienten sind.
Langzeitstabilität:
Alterung von Widerständen kann das Teilerverhältnis verschieben.
Metallfilmwiderstände sind stabiler als Kohleschichtwiderstände.
Hochfrequenz-Betrachtungen
Parasitäre Effekte:
- Kapazitäten: Zwischen Widerständen und zur Masse
- Induktivitäten: Bei Drahtwiderstänfden
- Frequenzgang: Tiefpass-Verhalten durch Parasitäten
Spezielle Spannungsteiler-Topologien
Kelvin-Spannungsteiler:
Vier-Draht-Messung zur Elimination von Leitungswiderständen bei Präzisionsmessungen.
Kompensierter Spannungsteiler:
Zusätzliche Kondensatoren parallel zu den Widerständen für konstantes
Frequenzverhalten (AC-gekoppelte Spannungsteiler).
Der Spannungsteiler ist eine der grundlegendsten und vielseitigsten Schaltungen in der Elektrotechnik. Von einfachen Referenzspannungen bis zu komplexen Messschaltungen - das Verständnis der Spannungsaufteilung und der praktischen Limitierungen ist essentiell für jeden Schaltungsentwickler. Die korrekte Dimensionierung unter Berücksichtigung von Last, Genauigkeit und Stabilität ist entscheidend für erfolgreiche Anwendungen.
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode