RC-Differenzierer Rechner
Berechnung von RC-Differenziergliedern: Widerstand, Kapazität, Zeitkonstante und Impulsverhalten
Zur Berechnung wählen Sie zunächst mit den Button aus, was Sie berechnen möchten. Danach geben Sie die Werte für Widerstand, Kondensator oder Frequenz/Periodendauer ein.
RC-Differenzierer verstehen
Ein RC-Differenzierer ist ein Impulsformer, der aus Rechteckspannungen am Eingang scharfe, nadelförmige Impulse am Ausgang erzeugt. Er besteht aus einem Kondensator C in Serie mit dem Eingang und einem Widerstand R parallel zum Ausgang. Die Zeitkonstante τ = RC bestimmt die Form der Ausgangsimpulse.
⏰ Zeitkonstante τ
Bestimmt die Impulsform:
📊 Impulsform-Kriterium
Für optimale Differenzierung:
⚡ Dimensionierung
Für t₁ = 5τ (optimale Form):
🎯 Spitze Impulse
Für t₁ ≫ 10τ (sehr spitze Impulse):
Grundformeln des RC-Differenzierers
📊 Zeitkonstante und Dimensionierung
Die fundamentalen Beziehungen für den RC-Differenzierer:
\[τ = R \cdot C\] \[R = \frac{τ}{C} = \frac{t_1}{nC}\] \[C = \frac{τ}{R} = \frac{t_1}{nR}\]
Wobei: n = 5 für optimale Form, n = 10 für spitze Impulse
🔧 Ausgangsspannung
Die Ausgangsspannung für verschiedene Eingangssignal-Formen:
\[u_{aus}(t) = RC \cdot \frac{du_{ein}}{dt}\] \[\text{Für Rechteckimpuls: } u_{aus} = U_0 \cdot e^{-t/τ}\]
Bei Flankenübergängen: Ausgangsspannung = ±Eingangsspannung
Praktische Beispiele
📝 Beispiel 1: Impulsspitzer für Digitalsignale
Aufgabe: 1 kHz Rechtecksignal mit 0,5 ms Impulsdauer schärfen
Gegeben: t₁ = 0,5 ms, Verhältnis t₁/τ = 5, gesucht: R und C
Berechnung:
\[τ = \frac{t_1}{5} = \frac{0,5 \text{ ms}}{5} = 0,1 \text{ ms}\] \[\text{Wähle } C = 100 \text{ nF} \Rightarrow R = \frac{τ}{C} = \frac{0,1 \times 10^{-3}}{100 \times 10^{-9}} = 1 \text{ kΩ}\]
Ergebnis: R = 1 kΩ, C = 100 nF erzeugt symmetrische +/- Impulse.
📝 Beispiel 2: Trigger-Impulse für Flipflops
Aufgabe: Sehr kurze Trigger-Impulse aus 10 ms Rechteckwelle
Gegeben: t₁ = 10 ms, sehr spitze Form gewünscht (t₁/τ = 20)
Berechnung:
\[τ = \frac{t_1}{20} = \frac{10 \text{ ms}}{20} = 0,5 \text{ ms}\] \[\text{Wähle } R = 10 \text{ kΩ} \Rightarrow C = \frac{τ}{R} = \frac{0,5 \times 10^{-3}}{10 \times 10^3} = 50 \text{ nF}\]
Ergebnis: R = 10 kΩ, C = 50 nF erzeugt sehr kurze Nadelimpulse.
Schaltbild und Signalverläufe
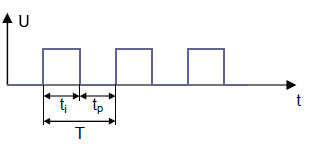
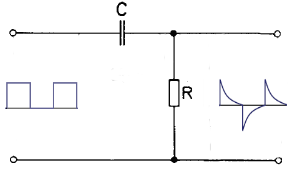
📈 Signalverhalten t₁ = 5τ
- • Anstiegsflanke: +U₀ Impuls
- • Abfallflanke: -U₀ Impuls
- • Impulsdauer: ≈ 3τ
- • Form: Exponentieller Abfall
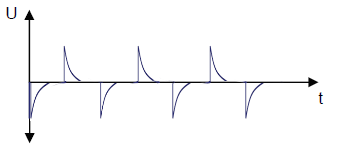
📐 Signalverhalten t₁ ≫ 10τ
- • Anstiegsflanke: Kurzer +U₀ Spike
- • Abfallflanke: Kurzer -U₀ Spike
- • Impulsdauer: ≈ τ
- • Form: Sehr spitze Nadelimpulse

Praktische Anwendungen
💻 Digitaltechnik
- • Trigger-Impulse für Flipflops
- • Clock-Edge-Detection
- • Impulsverkürzung
- • Reset-Impulsgenerierung
📡 Signalverarbeitung
- • Kantenerkkennung
- • Hochpass-Kopplung
- • Impulsformung
- • AC-Kopplung
💡 Praktische Tipps:
- Dimensionierung: τ sollte 5-20x kleiner als die Impulsdauer sein
- Kondensator-Wahl: Schnelle Typen (Keramik, Folie) für hohe Frequenzen
- Lastimpedanz: Nachfolgeschaltung sollte hochohmig sein (≥10×R)
- DC-Verhalten: Keine Gleichspannungsübertragung möglich
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode