Zenerdiode Vorwiderstand Rechner - Variable Last
Berechnung von Zenerdioden-Vorwiderständen mit variabler Belastung und optimaler Dimensionierung
Geben Sie die Eingangsspannung, gewünschte Ausgangsspannung (Zenerspannung) und den Laststrom-Bereich ein und klicken Sie auf Berechnen um den optimalen Vorwiderstand und die kritischen Leistungen zu ermitteln.
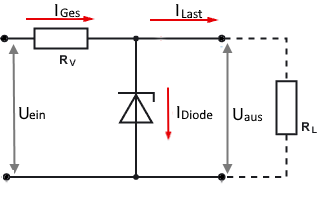
Zenerdiode mit variabler Last
Spannungsregelung bei schwankenden Lastströmen
Zenerdiode mit variabler Last verstehen
Zenerdioden mit variabler Last sind eine Herausforderung der Spannungsregelung. Der Gesamtstrom durch den Vorwiderstand bleibt konstant, aber die Stromaufteilung zwischen Last und Zenerdiode ändert sich. Bei geringer Last fließt mehr Strom durch die Zenerdiode, bei hoher Last weniger. Die Zenerdiode muss für den maximalen Strom dimensioniert werden.
⚡ Stromkompensation
Konstanter Gesamtstrom:
🔥 Kritische Leistung
Maximum bei ILast = Minimum:
✅ Vorteile variabler Last
- • Automatische Laststrom-Kompensation
- • Stabile Ausgangsspannung trotz Lastschwankung
- • Einfache Schaltung ohne Regelschaltkreis
- • Robuste und zuverlässige Funktion
⚠️ Herausforderungen
- • Hohe Verlustleistung bei kleinen Lasten
- • Thermische Dimensionierung kritisch
- • Mindest-Zenerstrom für Stabilität nötig
- • Schlechte Effizienz bei geringer Last
Formeln für variable Zenerdioden-Last
⚡ Gesamtstrom berechnen
Konstanter Strom durch den Vorwiderstand:
\[I_{ges} = I_{Zener,min} + I_{Last,max}\] \[I_{Zener,min} = 0,1 \times I_{Last,max} \text{ (Richtwert 10%)}\] \[\text{Beispiel: } I_{ges} = 10mA + 100mA = 110mA\]
IGes: Bestimmt die Dimensionierung des Vorwiderstands
🔧 Vorwiderstand dimensionieren
Widerstand für konstanten Gesamtstrom:
\[R_v = \frac{U_{ein} - U_Z}{I_{ges}}\] \[P_{Rv} = (U_{ein} - U_Z) \times I_{ges}\] \[\text{Beispiel: } R_v = \frac{12V - 5,1V}{110mA} = \frac{6,9V}{0,11A} = 62,7\Omega\]
E-Reihe: 68Ω wählen für sichere Dimensionierung
🔥 Kritische Zenerdioden-Leistung
Maximum bei geringstem Laststrom:
\[I_{Zener,max} = I_{ges} - I_{Last,min}\] \[P_{Zener,max} = U_Z \times I_{Zener,max}\] \[\text{Bei } I_{Last,min} = 0: P_{Zener,max} = 5,1V \times 110mA = 0,56W\] \[\text{Zenerdiode wählen: } P_{Zener} \geq 1W \text{ (Sicherheitsfaktor 2)}\]
Praktische Berechnungsbeispiele
📝 Beispiel 1: Mikrocontroller-Versorgung
Aufgabe: 5V-Regelung für µC mit variabler Last
Gegeben: Uein = 9V, UZ = 5,1V, ILast = 0-80mA
Berechnung:
\[I_{Zener,min} = 0,1 \times 80mA = 8mA\] \[I_{ges} = 8mA + 80mA = 88mA\] \[R_v = \frac{9V - 5,1V}{88mA} = \frac{3,9V}{0,088A} = 44,3\Omega \rightarrow 47\Omega\] \[P_{Zener,max} = 5,1V \times 88mA = 0,45W \rightarrow 1W \text{ Zenerdiode}\]
Lösung: 47Ω/0,5W + 5,1V/1W Zenerdiode
📝 Beispiel 2: LED-Anzeige mit Ein/Aus
Aufgabe: 3,3V für LEDs die ein-/ausgeschaltet werden
Gegeben: Uein = 5V, UZ = 3,3V, ILast = 0-150mA (schaltbar)
Berechnung:
\[I_{Zener,min} = 0,15 \times 150mA = 22,5mA\] \[I_{ges} = 22,5mA + 150mA = 172,5mA\] \[R_v = \frac{5V - 3,3V}{172,5mA} = \frac{1,7V}{0,1725A} = 9,86\Omega \rightarrow 10\Omega\] \[P_{Zener,max} = 3,3V \times 172,5mA = 0,57W \rightarrow 1W\]
Problem: Sehr hohe Verlustleistung! Schaltregler wäre effizienter.
📝 Beispiel 3: Referenzspannung mit minimaler Last
Aufgabe: Präzise 6,8V Referenz für ADC
Gegeben: Uein = 15V, UZ = 6,8V, ILast = 0,1-2mA (hochohmig)
Berechnung:
\[I_{Zener,min} = 5mA \text{ (für stabile Referenz)}\] \[I_{ges} = 5mA + 2mA = 7mA\] \[R_v = \frac{15V - 6,8V}{7mA} = \frac{8,2V}{0,007A} = 1171\Omega \rightarrow 1,2k\Omega\] \[P_{Zener,max} = 6,8V \times 6,9mA = 47mW \rightarrow 0,5W\]
Optimal: Geringe Verluste, stabile Präzisions-Referenz
Zenerdioden-Auswahl und Kennwerte
📊 Standard-Zenerspannungen
- • 3,3V: Moderne Logik-Versorgung
- • 5,1V: TTL-Logik-Versorgung
- • 6,8V: Präzisions-Referenz
- • 9,1V: Hohe Spannungsregelung
- • 12V: Analog-Schaltkreise
🔥 Leistungsklassen
- • 0,5W: BZX55 (DO-35) kleine Gehäuse
- • 1W: BZX85 (DO-41) Standard
- • 5W: BZV56 (DO-201) größere Verluste
- • 20W: BZV57 (TO-220) mit Kühlkörper
Anwendungsgebiete
🖥️ Digital-Elektronik
- • Mikrocontroller mit variabler Aktivität
- • Logic-Level-Konverter
- • Schaltbare LED-Anzeigen
- • Sensor-Versorgungen
📊 Analog-Anwendungen
- • Referenzspannungen für ADCs
- • Op-Amp Versorgungen
- • Komparator-Schwellen
- • Trigger-Schaltungen
🔋 Batterie-Anwendungen
- • Überspannungsschutz
- • Lade-Spannungsbegrenzung
- • Backup-Versorgungen
- • Notfall-Beleuchtung
⚡ Automotive/Industrie
- • KFZ-Bordnetz-Regelung
- • Industrie-Sensor-Versorgung
- • Überspannungsschutz 24V
- • Robuste Umgebungen
💡 Praktische Dimensionierungsregeln:
- Mindest-Zenerstrom: 10-20% vom maximalen Laststrom für stabile Regelung
- Leistungsreserve: Zenerdiode mit doppelter berechneter Verlustleistung
- Temperaturgang: ~0,1%/°C berücksichtigen bei Präzisions-Anwendungen
- Widerstand E-Reihe: Nächsthöheren Wert für sicheren Betrieb wählen
⚠️ Wichtige Grenzen und Alternativen:
- Effizienz: Bei großen Lastvariationen sehr verlustreich
- Alternative: Schaltregler für bessere Effizienz bei >1W Verlustleistung
- Wärmeableitung: Bei >0,5W Kühlkörper oder größeres Gehäuse nötig
- Mindestlast nie unterschreiten: Sonst Zenerdioden-Überlastung
Effizienz-Vergleich: Zenerdiode vs. Schaltregler
⚡ Zenerdioden-Regelung
- • Effizienz: 40-70% (lastabhängig)
- • Vorteile: Einfach, robust, rauscharm
- • Kosten: Sehr niedrig
- • Geeignet für: <1W, konstante Last
🔄 Schaltregler (LDO/Buck)
- • Effizienz: 85-95% (konstant)
- • Vorteile: Hohe Effizienz, niedrige Verluste
- • Kosten: Höher (IC + Spule/Kondensatoren)
- • Geeignet für: >1W, variable Last
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode