LR-Parallelschaltung Rechner
Berechnung von LR-Parallelschaltungen: Admittanz, Ströme, Impedanz, Leistung und Phasenwinkel
Geben Sie die Werte für Induktivität L, Widerstand R, Frequenz f und Spannung U ein und klicken Sie auf Berechnen um die LR-Parallelschaltung zu analysieren.
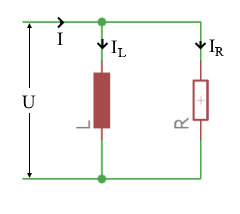
LR-Parallelschaltung verstehen
In einer LR-Parallelschaltung sind Widerstand R und Induktivität L parallel geschaltet. Die Spannung ist überall gleich, während sich die Ströme vektoriell addieren. Die Admittanz Y = √(G² + BL²) bestimmt das Leitverhalten der Schaltung.
⚡ Parallelschaltung-Prinzip
Grundlegende Eigenschaften:
🔄 Admittanz-Berechnung
Gesamtleitwert:
🔄 Strombeziehungen
Stromaufteilung:
📊 Impedanz-Beziehung
Gesamtimpedanz:
Grundformeln der LR-Parallelschaltung
📊 Stromdreieck
Vektorielle Addition der Teilströme:
\[I = \sqrt{I_R^2 + I_L^2}\] \[I_R = \frac{U}{R} = I \cdot \cos(φ)\] \[I_L = \frac{U}{X_L} = I \cdot \sin(φ)\] \[φ = \arctan\left(\frac{I_L}{I_R}\right)\]
🔧 Leitwertdreieck
Admittanz-Berechnung und Komponenten:
\[Y = \sqrt{G^2 + B_L^2} = \frac{1}{Z}\] \[G = \frac{1}{R} = Y \cdot \cos(φ)\] \[B_L = \frac{1}{X_L} = Y \cdot \sin(φ)\] \[Z = \frac{R \cdot X_L}{\sqrt{R^2 + X_L^2}}\]
⚡ Leistungsdreieck
Wirk-, Blind- und Scheinleistung:
\[S = \sqrt{P^2 + Q^2} = U \cdot I\] \[P = U \cdot I_R = \frac{U^2}{R}\] \[Q = U \cdot I_L = \frac{U^2}{X_L}\] \[\cos(φ) = \frac{P}{S} = \frac{I_R}{I}\]
Praktische Beispiele
📝 Beispiel 1: Leistungsfaktor-Korrektur
Aufgabe: Motor mit induktiver Last soll kompensiert werden
Gegeben: R = 10 Ω, L = 20 mH, f = 50 Hz, U = 230 V
Berechnung:
\[X_L = 2π \cdot 50 \cdot 20 \times 10^{-3} = 6,28 \text{ Ω}\] \[I_R = \frac{230}{10} = 23 \text{ A}, \quad I_L = \frac{230}{6,28} = 36,6 \text{ A}\] \[I = \sqrt{23^2 + 36,6^2} = 43,4 \text{ A}\] \[φ = \arctan\left(\frac{36,6}{23}\right) = 58°\]
Ergebnis: Gesamtstrom 43,4 A bei 58° Phasenverschiebung.
📝 Beispiel 2: Messschaltung mit Shunt
Aufgabe: Strommessung mit paralleler Drossel zur Frequenzanalyse
Gegeben: RShunt = 0,1 Ω, L = 100 μH, f = 1 kHz, U = 1 V
Berechnung:
\[X_L = 2π \cdot 1000 \cdot 100 \times 10^{-6} = 0,628 \text{ Ω}\] \[Z = \frac{0,1 \cdot 0,628}{\sqrt{0,1^2 + 0,628^2}} = 0,099 \text{ Ω}\] \[I = \frac{1}{0,099} = 10,1 \text{ A}\]
Ergebnis: Gesamtwiderstand 0,099 Ω, praktisch nur Shunt-Widerstand wirksam.
Eigenschaften und Verhalten
📈 Frequenzverhalten
- • DC (f=0): Z = R, nur resistiver Strom
- • Niedrige f: XL klein, IL groß
- • Hohe f: XL groß, IL klein
- • f → ∞: Z → R, nur resistiver Pfad
🔄 Phasenbeziehungen
- • IR: In Phase mit Spannung
- • IL: -90° zur Spannung
- • Iges: -φ zur Spannung
- • Leistung: Nur R verbraucht Wirkleistung
Praktische Anwendungen
🏭 Energietechnik
- • Leistungsfaktor-Korrektur
- • Parallele Motorwicklungen
- • Blindleistungskompensation
- • Drosselspulen-Arrays
📡 Messtechnik
- • Shunt-Schaltungen mit Induktivität
- • Frequenzselektive Messungen
- • Impedanzanalyse
- • Sensor-Linearisierung
💡 Praktische Tipps:
- Leitwerte nutzen: Bei Parallelschaltung sind Leitwerte einfacher zu rechnen
- Frequenzabhängigkeit: Bei niedrigen Frequenzen dominiert der induktive Zweig
- Leistungsfaktor: Parallelschaltung kann zur Kompensation genutzt werden
- Messgenauigkeit: Induktive Einflüsse bei Shunt-Messungen beachten
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode