Einweggleichrichter Rechner
Berechnung von Einweggleichrichtern: Effektivspannung, Mittelspannung und Spannungsverluste
Geben Sie die Eingangsspannung (Effektiv- oder Spitzenspannung) und die Diodenspannung ein und klicken Sie auf Berechnen um die Ausgangsspannungen des Einweggleichrichters zu ermitteln.
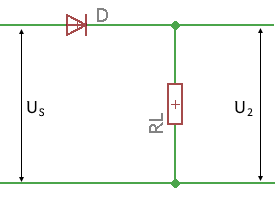
Einweggleichrichter verstehen
Der Einweggleichrichter ist die einfachste Art einer Gleichrichtung und besteht aus nur einer Diode. Am Lastwiderstand kommen nur die positiven Halbwellen der Eingangsspannung an, die negativen werden von der Diode "weggeschnitten". Dies ergibt eine pulsierende Gleichspannung mit großer Welligkeit.
⚡ Grundprinzip
Funktionsweise:
📊 Spannungswerte
Wichtige Beziehungen:
✅ Vorteile
- • Einfachster Aufbau (nur 1 Diode)
- • Geringe Kosten
- • Ohne Mittelpunkt-Trafo möglich
- • Geringer Spannungsabfall (1× UD)
❌ Nachteile
- • Sehr große Welligkeit
- • Schlechte Trafo-Ausnutzung
- • Hoher Glättungsaufwand
- • Gleichstromanteil im Trafo
Grundformeln der Einweggleichrichtung
⚡ Spannungsbeziehungen
Ausgangsspannung und Verluste:
\[U_2 = U_S - U_D\] \[U_S = U_{eff} \cdot \sqrt{2} \text{ (Spitzenspannung)}\] \[U_D = 0,7 \text{ V (Si-Diode)}\]
U₂: Spitzenspannung hinter der Diode
📊 Mittelwert und Effektivwert
Berechnung der Ausgangsspannungen:
\[U_{mittel} = \frac{U_2}{\pi} \approx 0,318 \cdot U_2\] \[U_{eff} = \frac{U_2}{2} = 0,5 \cdot U_2\] \[\text{Formfaktor: } \frac{U_{eff}}{U_{mittel}} = \frac{\pi}{2} \approx 1,57\]
🌊 Welligkeit und Ripple
Kennwerte der pulsierenden Gleichspannung:
\[\text{Welligkeit: } r = \frac{U_{wechsel}}{U_{mittel}} = \sqrt{\left(\frac{U_{eff}}{U_{mittel}}\right)^2 - 1}\] \[r = \sqrt{1,57^2 - 1} \approx 1,21 = 121\%\] \[\text{Grundfrequenz: } f_{ripple} = f_{netz}\]
Signalverläufe
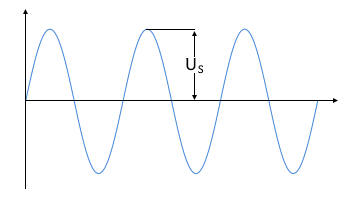
Eingangsspannung US
Sinusförmige Wechselspannung
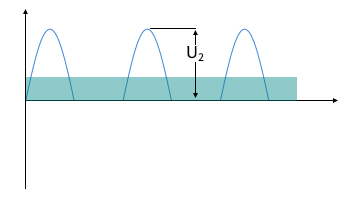
Ausgangsspannung U₂
Positive Halbwellen, pulsierende Gleichspannung
Praktische Beispiele
📝 Beispiel 1: 12V-Netzteil
Aufgabe: Einfaches 12V-Netzteil mit Einweggleichrichtung
Gegeben: Ueff = 15 V (Sekundärspannung), UD = 0,7 V
Berechnung:
\[U_S = 15 \cdot \sqrt{2} = 21,2 \text{ V}\] \[U_2 = 21,2 - 0,7 = 20,5 \text{ V}\] \[U_{mittel} = \frac{20,5}{\pi} = 6,5 \text{ V}\] \[U_{eff} = \frac{20,5}{2} = 10,25 \text{ V}\]
Ergebnis: Ausgangsspannung nur 6,5 V DC (viel zu niedrig für 12V-Netzteil).
📝 Beispiel 2: LED-Notbeleuchtung
Aufgabe: Einfache LED-Schaltung mit Einweggleichrichtung
Gegeben: Ueff = 6 V, UD = 0,7 V, ULED = 3,3 V
Berechnung:
\[U_S = 6 \cdot \sqrt{2} = 8,49 \text{ V}\] \[U_2 = 8,49 - 0,7 = 7,79 \text{ V}\] \[U_{mittel} = \frac{7,79}{\pi} = 2,48 \text{ V}\] \[\text{Spitzenspannung an LED: } 7,79 - 3,3 = 4,49 \text{ V}\]
Ergebnis: LED blinkt mit 50 Hz, mittlere Spannung zu niedrig für dauerhaften Betrieb.
Praktische Anwendungen
💡 Einfache Anwendungen
- • Batterieladegeräte (einfachste Bauart)
- • LED-Treiber mit PWM-Simulation
- • Spannungsvervielfacher (Cockroft-Walton)
- • Spitzenwertgleichrichter
🔬 Spezialanwendungen
- • HF-Gleichrichtung (Funkempfänger)
- • Spannungsdetektor für AC
- • Einfache Schutzschaltungen
- • Kondensator-Ladepumpen
⚠️ Wichtige Hinweise:
- Hohe Welligkeit: Ausgangsspannung pulsiert stark (121% Ripple)
- Schlechte Effizienz: Nur 50% der Eingangsleistung wird genutzt
- Trafo-Belastung: Gleichstromanteil führt zur Kernsättigung
- Glättung erforderlich: Großer Kondensator oder Drossel nötig
💡 Praktische Tipps:
- Diodenauswahl: Schottky-Dioden für niedrigere Verluste (0,3V statt 0,7V)
- Glättung: Großer Elektrolytkondensator parallel zur Last
- Strombegrenzung: Vorwiderstand oder Drossel zur Strombegrenzung
- Anwendung: Nur für unkritische Anwendungen mit geringen Anforderungen
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode