RCL Parallelschwingkreis Rechner
Berechnung von Parallelschwingkreisen: Resonanzfrequenz, Güte, Bandbreite und Stromüberhöhung
Geben Sie die Werte für Induktivität L, Kapazität C, Widerstand R und Spannung U ein und klicken Sie auf Berechnen um alle Parameter des Parallelschwingkreises zu ermitteln.
RCL-Parallelschwingkreis verstehen
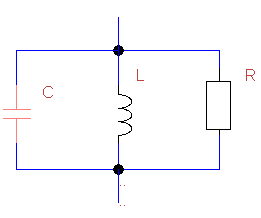
Ein RCL-Parallelschwingkreis besteht aus einem Widerstand R, einer Induktivität L und einer Kapazität C in Parallelschaltung. Er wirkt als Bandsperre (Sperrkreis), der Frequenzen in der Nähe der Resonanzfrequenz sperrt. Bei Resonanz ist die Impedanz maximal und es tritt Stromüberhöhung in L und C auf.
🚫 Resonanzbedingung
Bei Resonanz gilt:
📊 Güte und Stromüberhöhung
Qualitätsfaktor:
📏 Bandbreite
Sperrbereich:
🔄 Admittanz-Verhalten
Leitwert-Addition:
Grundformeln des RLC-Parallelschwingkreises
🌊 Resonanzfrequenz und Impedanz
Die grundlegenden Beziehungen bei Resonanz:
\[f_0 = \frac{1}{2π\sqrt{LC}}\] \[Y = \sqrt{G^2 + (B_C - B_L)^2}\] \[\text{Bei Resonanz: } Z = R \text{ (maximal), da } B_L = B_C\] \[I_0 = \frac{U}{R} \text{ (minimal)}\]
Admittanz: Y = 1/Z, G = 1/R, BL = 1/XL, BC = 1/XC
📊 Güte und Dämpfung
Qualitätsfaktoren und Stromüberhöhung:
\[Q = \frac{R}{X_L} = \frac{R}{X_C} = \frac{I_L}{I} = \frac{I_C}{I}\] \[d = \frac{1}{Q} \text{ (Dämpfung)}\] \[I_L = I_C = Q \cdot I \text{ (Stromüberhöhung)}\]
Stromüberhöhung: Bei hoher Güte können IL und IC >> I sein!
📏 Bandbreite und Grenzfrequenzen
Frequenzverhalten und -3dB-Punkte:
\[b = \frac{f_0}{Q} = f_0 \cdot d\] \[f_{go} = f_0 + \frac{b}{2}, \quad f_{gu} = f_0 - \frac{b}{2}\] \[\text{Bei } f_g: \text{ } Z_g = \frac{Z_0}{\sqrt{2}}, \text{ } I_g = I_0 \cdot \sqrt{2}\]
Praktische Beispiele
📝 Beispiel 1: FM-Bandsperre 100 MHz
Aufgabe: Bandsperre für FM-Radio bei 100 MHz mit Q = 50
Gegeben: f₀ = 100 MHz, L = 100 nH, Q = 50
Berechnung:
\[C = \frac{1}{(2π \cdot 100 \times 10^6)^2 \cdot 100 \times 10^{-9}} = 25,3 \text{ pF}\] \[X_L = 2π \cdot 100 \times 10^6 \cdot 100 \times 10^{-9} = 62,8 \text{ Ω}\] \[R = Q \cdot X_L = 50 \cdot 62,8 = 3140 \text{ Ω}\] \[b = \frac{100 \times 10^6}{50} = 2 \text{ MHz}\]
Ergebnis: C = 25,3 pF, R = 3,14 kΩ, Bandbreite = 2 MHz.
📝 Beispiel 2: Audio-Notch-Filter 1 kHz
Aufgabe: Notch-Filter gegen 1 kHz Netzbrumm
Gegeben: f₀ = 1 kHz, C = 220 nF, R = 1 kΩ
Berechnung:
\[L = \frac{1}{(2π \cdot 1000)^2 \cdot 220 \times 10^{-9}} = 115 \text{ mH}\] \[X_L = 2π \cdot 1000 \cdot 0,115 = 723 \text{ Ω}\] \[Q = \frac{1000}{723} = 1,38\] \[b = \frac{1000}{1,38} = 725 \text{ Hz}\]
Ergebnis: L = 115 mH, Q = 1,38, Bandbreite = 725 Hz.
Parallelschwingkreis vs. Serienschwingkreis
🚫 Parallelschwingkreis
- • Funktion: Bandsperre/Sperrkreis
- • Resonanz: Maximale Impedanz
- • Strom: Minimal bei f₀, überhöht in L/C
- • Anwendung: Störfrequenzen ausfiltern
📊 Serienschwingkreis
- • Funktion: Bandpass/Durchlasskreis
- • Resonanz: Minimale Impedanz
- • Strom: Maximal bei f₀, konstant in L/C
- • Anwendung: Nutzfrequenzen durchlassen
Praktische Anwendungen
📻 Hochfrequenztechnik
- • Störsignal-Unterdrückung in Empfängern
- • Oberwellen-Filter in Sendern
- • Antennen-Saugkreise
- • EMV-Filter gegen Störemissionen
🔊 Audio-Technik
- • Notch-Filter gegen Netzbrumm
- • Feedback-Unterdrückung
- • Equalizer-Kerben
- • Anti-Resonanz in Lautsprechern
⚡ Leistungselektronik
- • Snubber-Netzwerke
- • EMI-Filter
- • Switching-Spike-Unterdrückung
- • DC/DC-Wandler-Filter
🔬 Messtechnik
- • Trap-Filter in Oszilloskopen
- • Störunterdrückung in Verstärkern
- • Frequenzselektive Dämpfung
- • Kalibrierungs-Standards
💡 Praktische Tipps:
- Güte-Optimierung: Hochwertige Spulen und Kondensatoren für scharfe Sperren
- Stromüberhöhung: Bauteil-Belastbarkeit bei hoher Güte beachten
- Temperaturstabilität: NP0/C0G-Kondensatoren für stabile Sperrfrequenz
- Güte vs. Bandbreite: Kompromiss zwischen Trennschärfe und Dämpfung
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode