Zenerdiode Vorwiderstand Rechner - Konstante Last
Berechnung von Zenerdioden-Vorwiderständen mit konstanter Belastung und präziser Dimensionierung
Geben Sie die Eingangsspannung, gewünschte Ausgangsspannung (Zenerspannung) und die konstante Last ein und klicken Sie auf Berechnen um den optimalen Vorwiderstand und die Verlustleistungen zu ermitteln.
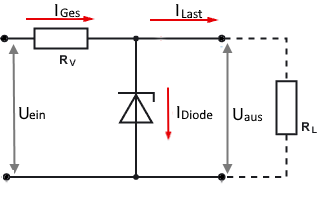
Zenerdiode mit konstanter Last
Optimale Spannungsregelung bei fester Belastung
Zenerdiode mit konstanter Last verstehen
Zenerdioden mit konstanter Last bieten die optimale Effizienz bei Spannungsreglerschaltungen. Da der Laststrom konstant ist, kann die Zenerdiode mit minimalem Strom betrieben werden - gerade genug für eine stabile Spannungsregelung. Dies führt zu minimalen Verlusten und maximaler Effizienz der gesamten Schaltung.
⚡ Optimale Effizienz
Minimaler Zenerstrom:
🎯 Präzise Dimensionierung
Exakte Berechnung möglich:
✅ Vorteile konstanter Last
- • Maximale Effizienz durch minimalen Zenerstrom
- • Präzise und einfache Dimensionierung
- • Minimale Verlustleistung und Wärmeentwicklung
- • Stabile und zuverlässige Spannungsregelung
⚠️ Wichtige Voraussetzungen
- • Last darf nicht schwanken oder ausfallen
- • Bei Lastausfall Zenerdioden-Überlastung
- • Nur für definierte, konstante Anwendungen
- • Alternative: Variable Last Rechner verwenden
Formeln für konstante Zenerdioden-Last
⚡ Optimaler Gesamtstrom
Minimaler Strom für maximale Effizienz:
\[I_{ges} = I_{Last} + I_{Zener,min}\] \[I_{Zener,min} = 0,1 \times I_{Last} \text{ (oder min. 5-10mA)}\] \[\text{Beispiel: } I_{ges} = 100mA + 10mA = 110mA\]
Effizienz: η = ILast / IGes = 100mA / 110mA = 91%
🔧 Präzise Vorwiderstand-Berechnung
Exakte Dimensionierung ohne Sicherheitsaufschlag:
\[R_v = \frac{U_{ein} - U_Z}{I_{ges}}\] \[P_{Rv} = (U_{ein} - U_Z) \times I_{ges}\] \[\text{Beispiel: } R_v = \frac{12V - 5,1V}{110mA} = \frac{6,9V}{0,11A} = 62,7\Omega\]
E-Reihe: 68Ω für sichere Reserven, aber 62Ω wäre optimal
🎯 Minimale Verlustleistungen
Optimierte Leistungsbilanz bei konstanter Last:
\[P_{Zener} = U_Z \times I_{Zener,min} = 5,1V \times 10mA = 51mW\] \[P_{Gesamt} = P_{Rv} + P_{Zener} + P_{Last}\] \[\eta = \frac{P_{Last}}{P_{Gesamt}} = \frac{U_Z \times I_{Last}}{(U_{ein} - U_Z) \times I_{ges} + U_Z \times I_{ges}}\] \[\eta = \frac{U_Z \times I_{Last}}{U_{ein} \times I_{ges}} = \frac{5,1V \times 100mA}{12V \times 110mA} = 38,6\%\]
Praktische Berechnungsbeispiele
📝 Beispiel 1: Präzisions-Referenzspannung
Aufgabe: 5V-Referenz für 12-Bit ADC
Gegeben: Uein = 15V, UZ = 5,6V, ILast = 2mA (konstant)
Berechnung:
\[I_{Zener,min} = 5mA \text{ (für stabile Referenz)}\] \[I_{ges} = 2mA + 5mA = 7mA\] \[R_v = \frac{15V - 5,6V}{7mA} = \frac{9,4V}{0,007A} = 1343\Omega \rightarrow 1,5k\Omega\] \[P_{Zener} = 5,6V \times 5mA = 28mW \rightarrow 0,5W\] \[\eta = \frac{2mA}{7mA} = 28,6\% \text{ (aber sehr stabil!)}\]
Optimal: Sehr geringe absolute Verluste, höchste Präzision
📝 Beispiel 2: Op-Amp Versorgung
Aufgabe: ±12V für Analog-Schaltkreis
Gegeben: Uein = 18V, UZ = 12V, ILast = 50mA (konstant)
Berechnung:
\[I_{Zener,min} = 0,1 \times 50mA = 5mA\] \[I_{ges} = 50mA + 5mA = 55mA\] \[R_v = \frac{18V - 12V}{55mA} = \frac{6V}{0,055A} = 109\Omega \rightarrow 120\Omega\] \[P_{Zener} = 12V \times 5mA = 60mW \rightarrow 0,5W\] \[\eta = \frac{50mA}{55mA} = 90,9\% \text{ (excellent!)}\]
Sehr gut: Hohe Effizienz bei moderaten Verlusten
📝 Beispiel 3: LED-Konstantstrom (ungünstig)
Aufgabe: 3,3V für High-Power LED
Gegeben: Uein = 24V, UZ = 3,3V, ILast = 1A (konstant)
Berechnung:
\[I_{Zener,min} = 0,1 \times 1A = 100mA\] \[I_{ges} = 1A + 100mA = 1,1A\] \[R_v = \frac{24V - 3,3V}{1,1A} = \frac{20,7V}{1,1A} = 18,8\Omega \rightarrow 22\Omega\] \[P_{Verlust} = 20,7V \times 1,1A = 22,8W \text{ (!!)}\] \[\eta = \frac{3,3V}{24V} = 13,8\% \text{ (schlecht!)}\]
Problem: Sehr hohe Verluste! Buck-Converter wäre besser (>90% Effizienz)
Anwendungsgebiete konstanter Zenerdioden-Last
📊 Präzisions-Anwendungen
- • Referenzspannungen für ADCs/DACs
- • Komparator-Schwellwerte
- • Präzisions-Messgeräte
- • Kalibrierstandards
🔬 Analog-Schaltungen
- • Op-Amp Hilfsversorgungen
- • Analog-Filter Versorgung
- • Instrumentenverstärker
- • Audio-Vorverstärker
🖥️ Digital konstant
- • FPGA-Core-Versorgung (konstant)
- • Crystal-Oszillator-Versorgung
- • Real-Time-Clock (RTC)
- • Immer-aktive Sensoren
🔧 Konstante Bias-Ströme
- • Transistor-Bias-Netzwerke
- • LED-Anzeigen (immer an)
- • Konstantstrom-Quellen
- • Temperatur-Kompensation
Effizienz-Optimierung bei konstanter Last
⚡ Zenerdioden-Regelung
- • Effizienz: UZ / Uein (theoretisch)
- • Praktisch: 40-90% je nach Spannungen
- • Vorteile: Einfach, rauscharm, präzise
- • Optimal bei: Niedrigen Strömen
🔄 Alternative: LDO-Regler
- • Effizienz: Ähnlich wie Zenerdiode
- • Vorteile: Bessere Regelung, einstellbar
- • Nachteile: Komplexer, teurer
- • Wann: Bei höheren Strömen >100mA
💡 Optimierungs-Tipps für konstante Last:
- Minimaler Zenerstrom: Nur soviel wie für Stabilität nötig (5-20mA)
- Spannungsverhältnis: UZ möglichst nahe an Uein für hohe Effizienz
- Präzisions-Zener: ±1% Toleranz für stabile Referenzen
- Temperaturgang: TK ≤ 0,05%/°C für Präzisionsanwendungen
🎯 Wann konstante Last optimal ist:
- Definierte Anwendung: Last ist immer konstant und bekannt
- Niedrige Ströme: Typisch <100mA für gute Effizienz
- Einfachheit gewünscht: Minimaler Schaltungsaufwand
- Präzision wichtig: Stabile, rauscharme Referenzspannung
Vergleich: Konstante vs. Variable Last
| Eigenschaft | Konstante Last | Variable Last |
|---|---|---|
| Effizienz | Optimal (bis 90%) | Lastabhängig (10-70%) |
| Zenerstrom | Minimal nötig | Maximal dimensioniert |
| Verlustleistung | Minimal | Bei geringer Last hoch |
| Dimensionierung | Exakt berechenbar | Für Worst-Case |
| Anwendung | Referenzen, Analog-ICs | µC, schaltbare LEDs |
| Sicherheit | Last darf nicht ausfallen | Robust bei Lastausfall |
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode